[Graphics] Transformation Pipeline (local ~ screen 좌표계)

Intro.
혹시 지금 무엇을 보고 계신가요?(아마 모니터겠죠?)
왼쪽과 오른쪽, 앞 뒤엔 무엇이 있나요?
제 기준에선 좌측엔 커피, 우측엔 가방이 있습니다. 다만, 제 앞에 계신분 입장에선 다를 것 같습니다.
저와 마주보고 있기에 그 분 기준에선 전방 우측에 제 가방, 전방 좌측에 제 커피 잔이 있습니다.
즉, 저희가 보는 세상은 1인칭, 나 자신을 기준으로 하는 상대 좌표계란 점이지요. (세상은 나 자신을 기준으로 돌고 있다!)
그럼 저 멀리 미국에 사는 John기준엔 저는 어디있을까요? (좌 -> 전 -> 우 -> 후 -> 우 -> 전 -> ...) 어딘가 있겠지요?
이런 좌표 시스템이 사실 컴퓨터 그래픽스에도 그대로 적용된답니다. (이 점이 너무 흥미로워서 사실 이 주제로 글을 쓰게 되었습니다)
각 model들의 고유 좌표계가 있고 이를 유저인 우리가 전능한 시점으로 최종 좌표계를 통해 각 model들을 관조하는 것이지요.
이번 글에선 model의 고유 좌표계가 어떤식으로 변형되어 최종 좌표계까지 어떻게 도달하는지 알아보려합니다.
** Background **
1. 3차원 그래픽에선 먼저 3차 동차좌표계 를 통해 좌표를 표현합니다.
What is Transformation Pipeline?
Transformation pipeline은 각 물체의 좌표계를 각 단계의 파이프라인을 거쳐 최종적으로 Screen space를 기준 좌표계를 얻는 과정입니다. 몇몇 과정은 변환 행렬과의 행렬곱을 통해 다음 과정으로 넘어 갑니다.
다음의 과정들로 이루어져 있습니다.
- Local Space
- World Space
- Camera Space
- Clip Space
- NDC space
- Screen Space
각 과정에 대해 설명하기 전에, 간단하게 변환 행렬들에 대해 알면 좋을거 같아 소개하겠습니다. ( 행렬 변환에 대해선 추후 다른 글로 알아가 보겠습니다.)
1. 이동 (Translation)

2. 회전 ( Rotation )
아래 방식은 오일러 변환 행렬인데 실제 사용 시, 짐벌락 (zimbal-lock)등의 이유로 quaternion을 회전 변환 할 때 사용하는 것으로 알고 있습니다.

3. 확대 / 축소 ( Scaling )

4. 반사 ( Reflection )
해당 변환을 적용할 좌표 축에 대해 적용하면 됩니다.

4. 역 변환 ( Inverse )

Local Space
Object space라고 칭하기도 하며, 우리 각 개인의 시점, 즉 상대 좌표계 입니다. 각 물체의 위치가 곧 원점입니다.
각 개별 물체의 vertex position를 정의하기 쉽기에 가장 기본적으로 사용합니다.
Model Matrix와의 곱 연산을 통해 , World Space를 구할 수 있습니다.

World Space
World space는 Scene의 중심을 원점으로 삼는 좌표계입니다. 각 오브젝트들을 Scene 기준으로 정렬시키기에 용이하기에 사용합니다.이해하기 쉽게 현실과 대응해보면, 구글 맵을 예시로 들 수 있을것 같습니다.
구글 맵에서 북쪽은, 아무리 돌고 뒤집고 해도 절대적으로 북쪽이지요?
위 local space 의 원점을 world space로 변환해 보겠습니다.

물체를 Z축 기준 30도 회전 후, (1,2,3) 평행이동의 결과는 다음과 같습니다. 행렬곱이기에 곱 순서에 주의합시다.

View Space
Camera Space 혹은 Eye Space라고 합니다. World space와 동일한 Scene이지만, 카메라의 위치에 맞게 좌표가 재정렬 됩니다. 컵을 바라볼때, 보는 위치나 방향에 따라 위치가 달라지지요? 여기서 컵을 보는 눈을 camera라고 생각하시면 됩니다. camera의 위치를 알고 있으니, localSpace -> World Space 변환 과정처럼 마찬가지로 이번엔 View(Camera) matrix를 곱하여 좌표계를 구하면 됩니다.
이를 통해, 컵의 좌표는 카메라를 기준으로 하여 변형되겠죠?
View Matrix는 다음과 같습니다. 음....뭔지 모르겠네요..? 한번 알아봅시다.
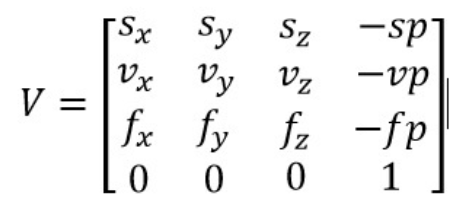
먼저 카메라 오브젝트 Local Space에선 카메라 위치는 원점이고, 카메라는 현재 -Z축 방향을 바라보고 있습니다. 다음 그림과 같습니다.
이제 카메라를 world space 어딘가에 놓겠습니다. 다음 그림처럼 말이죠

먼저 I , J , K 를 world space의 x, y, z 축이라 칭하겠습니다.
E = 카메라 위치
L = 카메라가 바라보는 지점
UP = 카메라의 UP 방향 벡터
를 알고 있는 상황에서
View matrix, 즉, 이 행렬을 이용한 변환은 결과적으로 물체를 카메라를 기준으로한 좌표계로 정렬할 것입니다. 따라서, 필연적으로 world space상 카메라 방향 벡터를 구해야합니다. 그리고 그것이 곧, view space의 좌표축이 되겠지요?
기본적으로 UP 벡터와 E와 L을 알고 있으니, 2가지 축을 알고 있는 셈입니다.
나머지 축은 N벡터와 UP벡터의 외적을 통해 구할 수 있습니다.
여기서 왜 E -> L 방향 벡터가 아닌 N 벡터를 기준 축으로 삼느냐?라 생각하실 수 있습니다만, 그 이유는 위에서 서술했듯, 카메라 Local좌표계상 카메라가 바라보고 있는 방향이 -Z축이기 때문입니다.
N = ( E - L )
U = N X UP
v = N X U ( 왜 이걸 구하냐 생각하실 수 도 있는데, N 과 UP이 수직임을 보장할 수 없기 때문에 구합니다)
그럼 View matrix (이하 V 행렬)은 다음과 같은 성질을 지니게 됩니다.
VU = I (World space Z)
Vv = J (World space Y)
VN = K (World space Z)
자! 이제 거의 다 왔습니다.

그럼 a , b ,c 는 어떻게 구할까요?
V가 카메라 위치 E를 O(0, 0 ,0)으로 변환시킨다는 성질을 이용하면 다음 처럼 나타낼 수 있습니다.
(e = E - O )

한번 예시를 들어볼까요?
eye = (10, 5, 5) , look = (0, 5 , 0), up = ( 1, 1 ,0)
(*p.s 모든 벡터를 정규화시키고 있기에, 각 벡터의 크기로 나누는 작업을 했습니다)
N = eye - look => (10, 0, 5) / √5
U = UP X N => (1, -1, 2) / √6
v = N X U => (1 ,5 , -2) / √30
e = E - O => (10 ,5 , 5)
-eu = -5 / √6
-ev = 25 / √30
-en = 25 / √5
Clip Space & NDC Space
저희가 사물을 볼 때, 무엇을 볼 수 있나요? 당연하지만 시야각 안에 포함된 물체만 눈에 보이겠죠?
이 과정에선, 카메라 영역 외 부분에 대한 cliping과 비로소 화면에 깊이감( 투영 )을 부여하는 작업이 일어납니다.
또한 이 과정의 결과값이 바로 vertex shader의 결과값입니다. ( model mat * view mat * projection mat , 그렇기에, Three.js 사용 시 , 이 과정까지 프로그래밍 가능하고, 이후 과정은 openGL에 맡기게 됩니다 )
(쓰면서 느낀건데... 쓰다보니 엄청 길어지네요... 그래도 일단 열심히 써넣어보려합니다)
저희가 3d 그래픽을 볼때, 사실 3차원을 본다기 보단, 2차원 평면 위에 투영된 이미지를 보는거지요?
Projection matrix의 경우 결과적으로 3d 공간상 물체들을 near plane 투영하여 에 2d화 시킨다 생각해도 될것 같습니다.
다음 그림을 참고해 주세요!
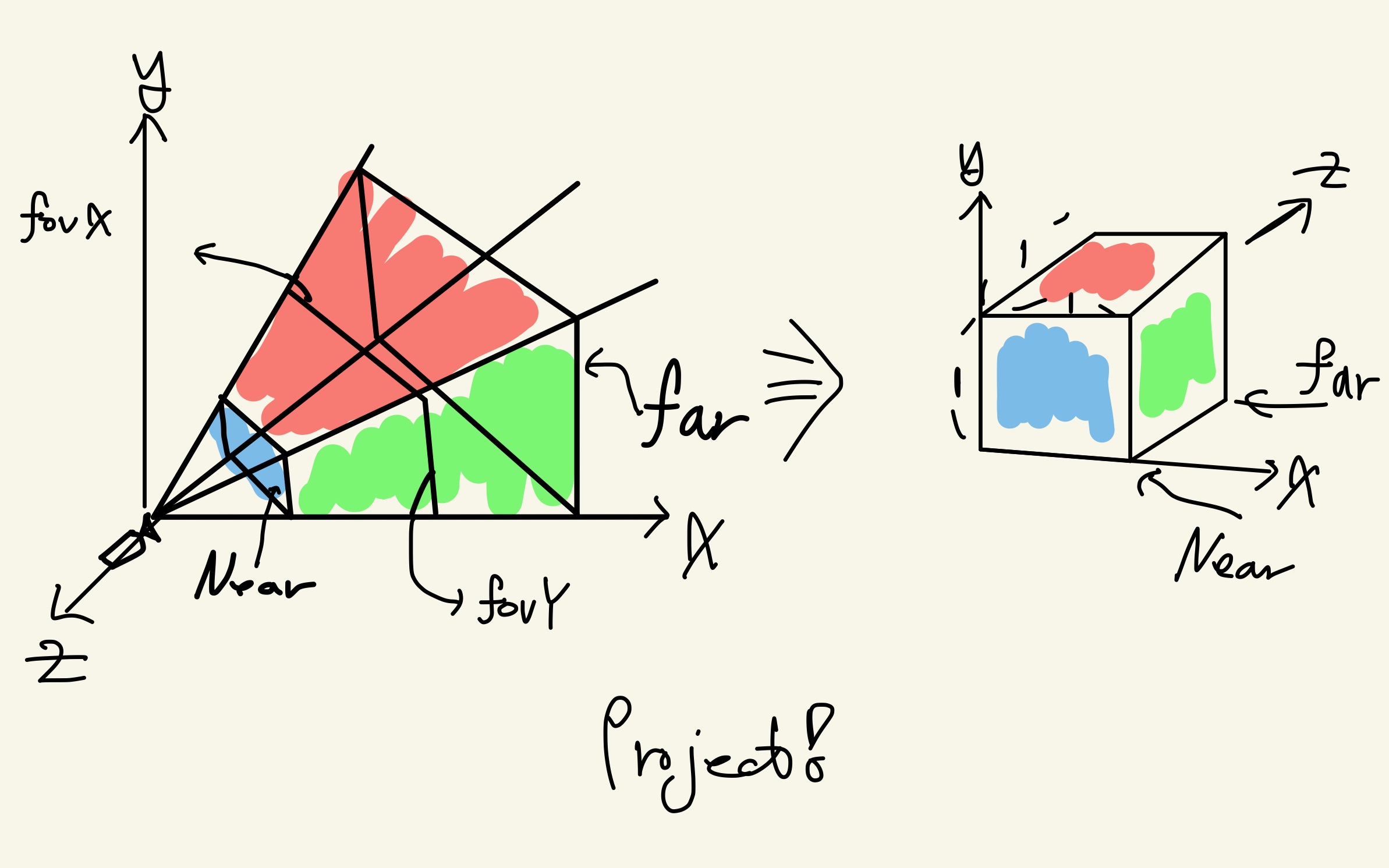
좌측 머리 잘린 사면체를 절두체(frustum)이라 부릅니다.
절두체 내부에 있는 물체들은 렌더링되고, 절두체 외부에 있는 물체들은 렌더링에서 제외됩니다. projection matrix의 결과로, 3 축 모두 (-1,1)의 범위를 갖는 정규화된 큐브모양의 공간이 생성되는데, 이를 NDC Space라 합니다.
그럼 어떻게해야 projection matrix를 만들 수 있을까요?
projection matrix = Orthogonal Projection matrix * perspective matrix 인데, 이번엔 perspective matrix에 대해 설명하겠습니다. (후에 orthogonal matrix도 추가할게요, 일단 이 글을 참고해주세요!)(https://www.scratchapixel.com/lessons/3d-basic-rendering/perspective-and-orthographic-projection-matrix/orthographic-projection-matrix.html)
원리를 설명하기 위해 간단한 예시를 들겠습니다.

2차원 동차 행렬을 대각 행렬 말고, 저런 행렬을 곱해주면 결과 값으로 [a,b,b]가 나옵니다.
차원값을 정상화 시키기 위해, b로 나눈다면 [a/b, 1 ,1]이 됩니다.
이를 그림으로 표현하면 다음과 같습니다.

위 그림에서, (2a,2b) 를 2b로 나누면, 동일 점으로 스케일링 가능하겠죠?
3차원 상에선 마찬가지로 동일 평면으로 스케일링이 가능합니다.

물체상 임의의 점을 near 평면에 투영시키고 싶습니다.
그럼 도형의 닮음 성질을 이용해, 투영점을 다음과 같이 표현할 수 있습니다. (Xs, Ys)는 투영된 점
Ys = (n / z) * Y
Xs = (n / z) * Y
따라서 perspective matrix P는 다음을 만족해야합니다.
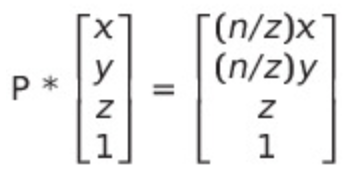
그런데 문제가 생겼습니다.
4X4행렬 연산 결과, 결과 벡터의 x,y를 z로 나누고, z를 유지시는 행렬이 존재하지 않기때문입니다.
다행히도, 저희는 지금 동차좌표계를 사용하고 있기에, 마지막 4번째 원소 w를 사용해, 이로써 perspective matrix P를 구해볼 수 있습니다.

오잉? 근데 왜 갑자기 z^2이 되지..???
만약 결과가 아래와 같다면(결과 벡터의 z값 = z)

w로 나눠질때, 3번째 행이 1이 됩니다. 즉, depth 정보를 유실하게 되는 셈이죠.
따라서 연산의 결과는 z^2가 되어야 후에 w로 나눌 때 깊이 정보가 보전됩니다.
이제 본격적으로 P를 구해 보겠습니다.
먼저 P의 1~2번째 행은, x,y값을 focal(카메라~ near plane까지 거리 )까지로 scaling해주는 역할입니다.
따라서 첫 두행은 다음과 같습니다.

4번째 행은 입력 벡터의 z를 결과 벡터의 4번째로 옮겨야하니 [0,0,1,0]이 될것입니다.
자 그럼 이제 3번째 행을 구해야합니다.

당연하지만, 첫번째와 두번째 열은 0입니다. 결과 벡터에 x,y가 포함이 안되니까요.
그럼 3,4번째 요소는 어떻게 구할까요? 편의상 m1,m2라 지칭하겠습니다.
near plane과 far plane의 특성을 이용해 2가지 방정식을 만들 수 있고, 이를 통해 연립방정식을 구성해, m1,m2를 구할 수 있습니다.
한번 생각해 봅시다. 애당초 near plane위에 있는 z값은 변환되어도 그 값이 변하지 않을 겁니다. far plane도 마찬가지고요.
따라서 다음과 같이 표현 가능합니다.

식을 정리하면 m1 = (f + n) , m2 = -f*n이 나옵니다.
이제 결과 벡터를 다시 정의하면 다음과 같습니다. ( nx , ny , (f+n)z - fn , w)
결과를 가지고 조금 돌이켜보겠습니다.

3번째 행의 값을 찾기 위해 적어도 near와 far 위치에선, 자기 자신으로 변환된다는 성질을 가지고 식을 짰습니다.
처음엔 이상적이도록 입력 벡터의 z값과 출력벡터의 z값이 1:1 대응인 선형 관계이길 원했습니다만, 결과적으로 (노란색 커브) 1:1 비선형이게 되었습니다.
하지만 괜찮습니다! 왜냐면 1:1 대응이기에 near ~ far 사이 상대적인 z값 순서는 유지되기 때문입니다.
또한 예기치 않는 장점이 있는데요, 그래프를 보다시피 near plane 근처의 z값은 high-precision을 얻기에, z - fighting 현상을 더 줄일 수 있습니다.
따라서 perspective projection matrix(orthogonal * perspective)는 다음과 같습니다.

여기서 식을 정리하기 위해 조금 더 고쳐보자면,
r = -l
t = -b
r+l = 0
b+t = 0
r- l = 2r
b-t = 2b
임과,
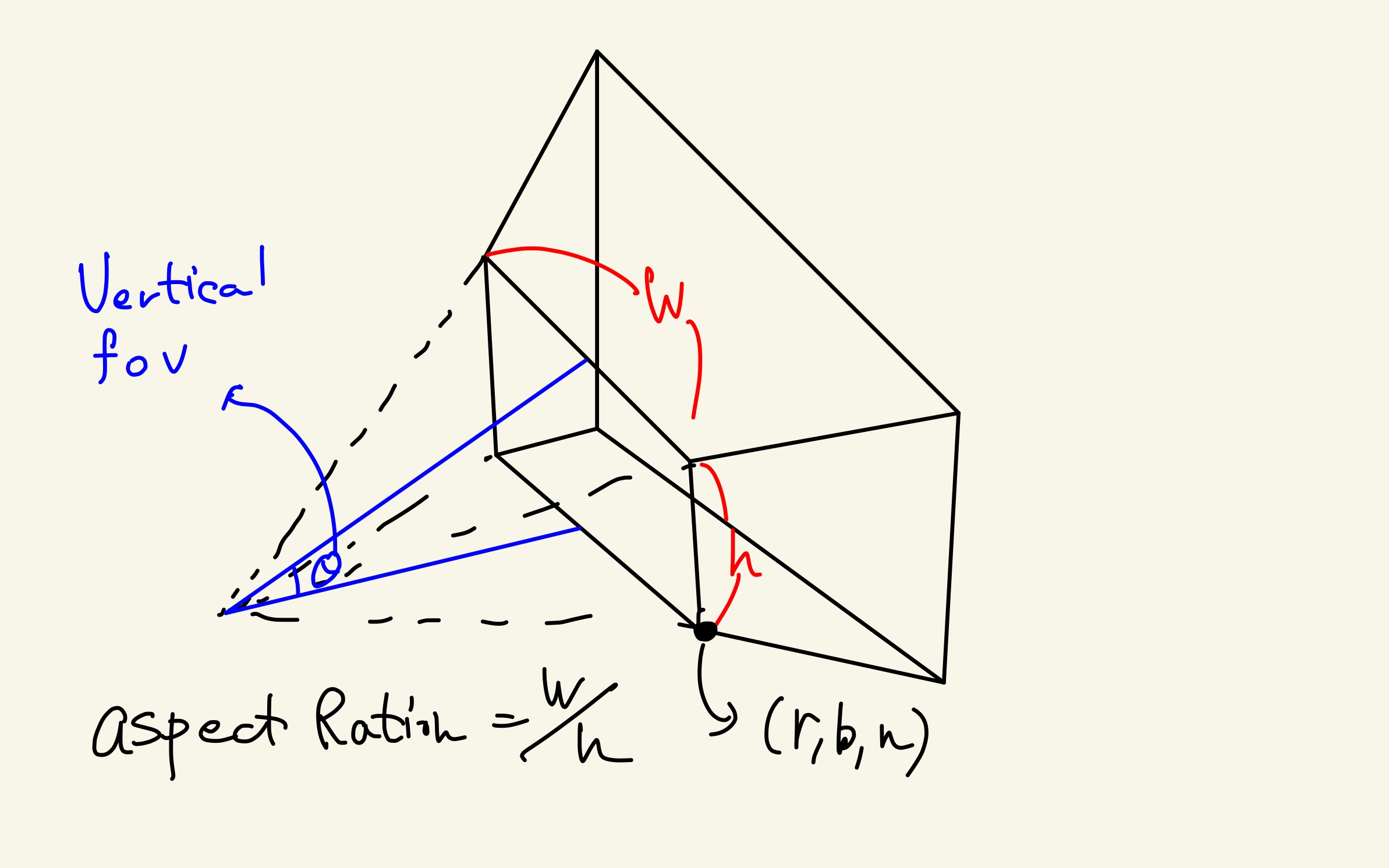
라 할 때,
b = n*tan(Θ / 2)
r = (nw / h) * tan(Θ / 2)
따라서, 기존 perspective projection matrix에 대응 시키면 저희가 아는 일반적인 공식이 나옵니다.

** 참고로 clipping이 어떻게 일어나는지에 대해선 다른 글로 소개하겠습니다. clipping algorithm의 종류과 꽤 많거든요..
Screen Space
드디어 ㅜㅜ 마지막 과정입니다. 변환에 얻어진 NDC space를 view port 디멘션에 맞게 늘려서 화면에 볼 수 있게 만드는 과정입니다.
여담이지만, 이 과정에서 rasterization이 일어납니다.

보다시피, x, y 가 viewport x,y로 확장 되는것을 볼 수 있고, z의 범위는 0 ~ 1로 재 편성 됩니다.
--------------
지적은 언제나 환영입니당 ㅎㅎ